Pokusil jsem se napsat Dijsktrův algoritmus pomocí LINQ konstrukcí. Pokud někdo z vás tápe, k čemu je Dijsktrův algoritmus dobrý a k čemu slouží, odkážu jej na podrobný článek na Wikipedii. Zde jen připomenu, že Dijsktrův algoritmus slouží k nalezení nejkratších cest v grafu z jednoho zdrojového uzlu ke všem ostatním uzlům. Je tak možné najít například nejkratší cestu z jednoho města do druhého. Na internetu jsem našel jeden graf, který budeme mít stále před očima a na který budeme Dijkstrův algoritmus napsaný v LINQu aplikovat.

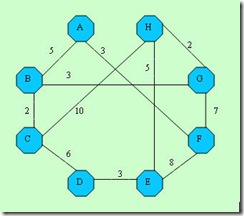
Uzly A, B atd. reprezentují města, ohodnocení hrany vyjadřuje počet kilometrů (město A je od města B vzdáleno 5 km). My budeme chtít spočítat nejkratší cestu z města H do města A a nebude nás zajímat jen počet ujetých kilometrů, ale také jak vypadá celá trasa - jinými slovy, přes jaká města naše nejkratší cesta vede.

Nejprve si vytvoříme potřebné třídy:

public interface IGraphEdge<T>
    {
        T From { get; }
        T To { get; }
        int Distance { get; }
    }

Rozhraní IGraphEdge reprezentuje hranu grafu - vlastnost From nám říká, odkud hrana vede (z města A), vlastnost To sděluje, kam hrana vede (město B). Vlastnost Distance nese vzdálenost mezi uzly (města A a B jsou vzdálena 5 km).

My pracujeme s vzdálenostmi mezi městy, a proto si vytvoříme jednoduchou třídu reprezentující město. Z města nás zajímá jen název.

class City : IEquatable<City>
    {
        private Guid Id;
        public City(string name)
        {
            Id = Guid.NewGuid();
            Name = name;
        }

        public string Name
        {
            get;
            set;
        }

        public override bool Equals(object obj)
        {
            City secondCity = obj as City;

            if (secondCity == null)
            {
                return false;
            }
            return Equals(secondCity);

        }

        public override int GetHashCode()
        {
            return Id.GetHashCode();
        }


        public bool Equals(City other)
        {
            if (other == null)
            {
                return false;
            }

            if (other.GetType() != this.GetType())
            {
                return false;
            }

            return (other.Id == Id);
        }

        public override string ToString()
        {
            return Name;
        }
    }

Hrany grafu představují silnice mezi městy, a proto si vytvoříme třídu CityEdge, která implemetuje rozhraní  IGraphEdge a za generický parametr T dosadí třídu City.

class CityEdge : IGraphEdge<City>
    {
        #region Implementation of IGraphNode<City>

        private City m_from;
        private City m_to;
        private int m_distance;

        public CityEdge(City from, City to, int distance)
        {
            if (from == null)
            {
                throw new ArgumentNullException("from");
            }

            if (to == null)
            {
                throw new ArgumentNullException("to");
            }

            if (distance <= 0)
            {
                throw new ArgumentException("value must be greater than zero", "distance");
            }

            m_from = from;
            m_distance = distance;
            m_to = to;
        }

        public City From
        {
            get
            {
                return m_from;
            }
        }

        public City To
        {
            get
            {
                return m_to;
            }
        }

        public int Distance
        {
            get
            {
                return m_distance;
            }
        }

        #endregion

        public override string ToString()
        {
            return String.Format("From: {0}, To {1}, Distance{2}", From, To, Distance);
        }


    }

Dále potřebujeme třídu, která ponese informaci o nalezené nejkratší cestě do daného bodu a o předchozím městu, přes které musíme cestovat. Na konkrétním příkladu - z města A (námi zvolený jediné výchozí město, z nějž se počítá nejkratší cesta ke všem ostatním městům) vede nejkratší cesta do města  C (vlastnost Current), která má délku 7 Km (vlastnost TotalDistance) a současně nám vlastnost Previous vrátí přechozí město (vlastnost Previous), přes které musíme jet (město B).

public class GraphPath<T> : IEquatable<GraphPath<T>>
    {
        private const int DUMMY_HASH_PLACEHOLDER = 100;
        
        public T Current
        {
            get;
            set;
        }

        public T Previous
        {
            get;
            set;
        }

        public int TotalDistance
        {
            get;
            set;
        }

        public override bool Equals(object obj)
        {
            GraphPath<T> second = obj as GraphPath<T>;

            if (second == null)
            {
                return false;
            }

            return Equals(second);

        }

        public override int GetHashCode()
        {
            var prevHash = (EqualityComparer<T>.Default.Equals(Previous, default(T)) ? DUMMY_HASH_PLACEHOLDER : Previous.GetHashCode());
            
            return (Current.GetHashCode() ^ prevHash ^ TotalDistance.GetHashCode());
        }

        #region Implementation of IEquatable<T>

        public bool Equals(GraphPath<T> other)
        {
            if (other == null)
            {
                return false;
            }

            if (other.GetType() != this.GetType())
            {
                return false;
            }

            return (EqualityComparer<T>.Default.Equals(Current, other.Current) &&
                    EqualityComparer<T>.Default.Equals(Previous, other.Previous) &&
                    TotalDistance.Equals(other.TotalDistance)
                    );
        }

        #endregion
    }

Přípravu máme za sebou, nyní se můžeme podívat na kostru celého algoritmu a poté rozpitvat jeho jednotlivé kroky. Pamatujme - důsledně se snažíme používat, kde to jen jde, LINQ konstrukce.

static void Main(string[] args)
        {
            var cities = (from i in Enumerable.Range(0, 8)
                          let key = ((char)(i + 'A')).ToString()
                          select new
                                     {
                                         Key = key,
                                         Value = new City(key)
                                     }).ToDictionary(el => el.Key, el => el.Value);




            var cityNodes = new List<CityEdge>
                                {
                                    new CityEdge(cities["A"], cities["B"], 5),
                                    new CityEdge(cities["A"], cities["F"], 3),
                                    new CityEdge(cities["B"], cities["C"], 2),
                                    new CityEdge(cities["B"], cities["G"], 3),
                                    new CityEdge(cities["C"], cities["H"], 10),
                                    new CityEdge(cities["C"], cities["D"], 6),
                                    new CityEdge(cities["D"], cities["E"], 3),
                                    new CityEdge(cities["E"], cities["H"], 5),
                                    new CityEdge(cities["E"], cities["F"], 8),
                                    new CityEdge(cities["F"], cities["G"], 7),
                                    new CityEdge(cities["G"], cities["H"], 2),
                                };


            var allCityNodes = cityNodes.Concat(from cn in cityNodes
                             select new CityEdge(cn.To, cn.From, cn.Distance)).ToArray();


            var resultPath = getShortestPath(cities["H"], allCityNodes);


            var pathFromTo = resultPath.EnumerateShortestPathTo(cities["H"], cities["A"]).Reverse();




            Array.ForEach(pathFromTo.ToArray(), myP =>
                                                Console.WriteLine("Přes město {0}, Ujetá vzdálenost: {1}", myP.Current, myP.TotalDistance));

            
            Console.ReadLine();
        }

Na začátku metody vygenerujeme objekt Dictionary (proměnná cities), kde klíčem je název města a hodnotou objekt City. Do proměnné cityNodes uložíme hrany grafu (existující silnice mezi městy) s jejich ohodnocenim (kilometry). Silnice ale nevede jen z města A do města B, ale také z města B do A, proto do proměnné allCityNodes uložíme i zpáteční cesty mezi městy. Poté voláme metodu getShortestPath, které předáme výchozí město (zde H), pro které chceme spočítat nejkratší cesty ke všem ostatním městům, a veškeré hrany-silnice. Metoda getShortestPat vrátí nejkratší cesty, nově vytvořené extenzní metodě EnumerateShortestPathTo řekneme, že chceme vypsat nejkratší cestu z města H (první argument) do města A (druhý argument) - metoda vrátí pouze města, přes která musíme jet z města H do města A a my metodou Reverse otočíme jejich pořadí, abychom viděli cestu od H do A a nezačínali koncovým městem A. Výsledek vypíšeme s využitím metody Array.ForEach na konzoli.

Skeleton algoritmu je hotov, čas začít nabalovat extenzní maso (doslova... ) a LINQ svaly.

Zde je metoda getShortestPath.

private static IEnumerable<GraphPath<A0>> getShortestPath<A0, A1>(A0 startPoint, IEnumerable<A1> nodes)
                                            where A1 : IGraphEdge<A0>
        {

            var initialGraphPath = (from cNode in nodes
                                    where !cNode.From.Equals(startPoint)
                                    select new GraphPath<A0>
                                    {

                                        Current = cNode.From,
                                        Previous = default(A0),
                                        TotalDistance = int.MaxValue

                                    }).Distinct();


            initialGraphPath = (initialGraphPath.Concat(from cNode in nodes
                                                       where cNode.From.Equals(startPoint)
                                                       select new GraphPath<A0>
                                                           {

                                                               Current = cNode.To,
                                                               Previous = startPoint,
                                                               TotalDistance = cNode.Distance

                                                           }));



            return getShortestPathInner(initialGraphPath, new[] { startPoint }, nodes);




        }

V metodě getShortestPath vygenerujeme objekty GraphPath, které po všech výpočtech ponesou nejkratší cestu v grafu. První dotaz vybere nejdříve ze seznamu hran pouze ty hrany, v nichž vlastnost From (Odkud) nepředstavuje počáteční město (where !cNode.From.Equals(startPoint) ). Jediné, co víme, je že vlastnost TotalDistance nového objektu GraphPath po ukončení algoritmu ponese informaci o nejkratší cestě z výchozího města do konkrétního města (vlastnost Current). U těchto uzlů tedy nejkratší vzdálenost neznáme, a proto vlastnost TotalDistance inicializujeme konstantou int.MaxValue, která říká "nejkratší cestu do města Current neznám a ještě ke všemu může být hodně dlouhá" . Z jednoho města může vést více silnic, což by vedlo k duplicitním objektům GraphPath, a proto pro každé město ponecháme pouze jeden objekt GraphPath voláním metody Distinct. 

K objektům  GraphPath z prvního dotazu připojíme objekty GraphPath  komplementárním dotazem, který vybere pouze ty hrany, v nichž vlastnost From (Odkud) představuje počáteční město (where !cNode.From.Equals(startPoint) ). Každý objekt GraphPath z druhého dotazu má tedy vlastnost TotalDistance rovnu kilometrům z fixně stanoveného počátečního města (vlastnost Previous - v našem příkladu město H) do města (Vlastnost Current), k němuž vede z H silnice přímo. Pro počáteční město H tedy druhý dotaz vrátí dva objekty GraphPath naplněné takto - {1 - Current=C, Previous=H, TotalDistance=10} {2-Current=E, Previous=H, TotalDistance=5}.

Poté zavoláme metodu getShortestPathInner, které předáme vygenerované objekty GraphPath, seznam objektů, pro něž jsme zjišťovali  nejkratší cestu v grafu (zatím jen počáteční město  - město H), a dříve vytvořený seznam hran.

private static IEnumerable<GraphPath<A0>> getShortestPathInner<A0, A1>(IEnumerable<GraphPath<A0>> initialGraphPath, IEnumerable<A0> processed, IEnumerable<A1> edges)
                                                        where A1 : IGraphEdge<A0>
        {
            var candidates = (from node in edges
                              where !processed.Contains(node.From)
                              select node.From).Distinct();

            if (candidates.Count() == 0)
            {
                return initialGraphPath;
            }

            var minimum = initialGraphPath.Where(gPath => candidates.Contains(gPath.Current)).Min(gPath => gPath.TotalDistance);

            var minimumGPath = (from gPath in initialGraphPath
                                where candidates.Contains(gPath.Current) &&
                                      gPath.TotalDistance == minimum
                                select gPath).First();



            var newGraphPath = from cNode in edges
                               where cNode.From.Equals(minimumGPath.Current)
                               select new GraphPath<A0>
                                       {

                                           Current = cNode.To,
                                           Previous = minimumGPath.Current,
                                           TotalDistance = cNode.Distance + minimumGPath.TotalDistance

                                       };



            var newGraphResult =
                                   (initialGraphPath.Concat(newGraphPath).Where(obj =>
                                                            !initialGraphPath.Any(
                                                                                   obj2 => obj2.Current.Equals(obj.Current) &&
                                                                                   (obj2.TotalDistance < obj.TotalDistance)))).ToArray();





            var newProcessed = processed.Union(new[] { minimumGPath.Current });

            return getShortestPathInner(newGraphResult, newProcessed, edges);

        }
    }

V rekurzivní metodě getShortestPathInner je soustředěno jádro Dijkstrova algoritmu. Do proměnné candidates uložíme nejprve veškerá města, která jsme ještě nezpracovali - nezjišťovali jsme, jak daleko je to od nich k jejich přímým sousedům. Do proměnné minimumGPath uložíme objekt GraphPath, který reprezentuje prozatímní nejkratší zjištěnou cestu z výchozího města a jehož vlastnost Current nese město, pro něž jsme výpočet nejkratší cesty ještě neprovedli.

Do proměnné newGraphPath uložíme množinu objektů GraphPath, které jsou sestaveny tak, že jejich předchůdcem (vlastnost Previous) je vždy právě zpracovávané město. Vlastnost To nese město, do něhož se můžeme dostat z města Previous. Vlastnost TotalDistance je inicializována součtem  hodnoty TotalDistance z procházeného objektu minimumGPath (s prozatímní nejkratší cestou) s vzdáleností z města v Previous do města ve vlastnosti Current.

Do proměnné newGraphPathResult jsou uloženy jen prozatím nejkratší cesty - jestliže tedy v předchozím kroku vypočítáme, že z města H se do města D můžeme dostat po ujetí 16 km, ale v proměnné initialGraphPath máme spočítáno, že do města H se můžeme dostat i po ujetí 8 km, je ponechána pouze lepší, tedy pro naše účely kratší cesta.

Poté na konci metody do seznamu již zpracovaných měst přidáme právě zpracované město (minimumGPath.Current) a jdeme na další kolo. Rekurzivně zavoláme metodu getShortestPathInner s vypočítanými mezivýsledky. Rekurze skončí po zpracování všech měst - nejsou  nalezeni další kandidáti na zpracování (viz podmínka if (candidates.Count() == 0 )).

Ještě nám zbývá extenzní metoda, která enumeruje přes města z výchozího bodu do cílového. První argument jsou vypočítané nejkratší cesty (objekty GraphPath), argument start je zvolené počáteční město a argument end je koncové město, ke kterému chceme vypsat nejkratší cestu.

static class DijkstraExtensions
    {
        public static IEnumerable<A0> EnumerateShortestPathTo<A0, A1>(this IEnumerable<A0> paths, A1 start, A1 end)
                                   where A0 : GraphPath<A1>
        {
            var pathDictionary = paths.ToDictionary(obj => obj.Current);
            var currentNode = pathDictionary[end];


            while (currentNode != null)
            {
                yield return currentNode;
                if (currentNode.Previous.Equals(start))
                {
                    yield break;
                }
                currentNode = pathDictionary[currentNode.Previous];
            }

        }
    }

Metoda si vytvoří další objekt Dictionary a postupně vrací veškerá objekty GraphPath na ceste z jednoho města (start) do druhého (end) tak, že v cyklu while z objektu Dictionary vyzvedává město-předchůdce (vlastnost Previous), přes které musíme jet, dokud se nedostaneme do výchozího města.

A zde je výsledek - nejkratší cesta z H do A.

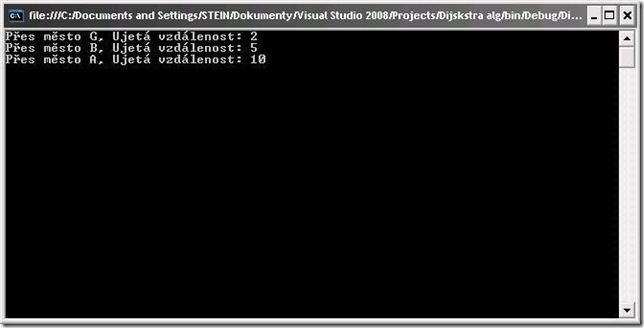
Použité algoritmy, LINQ konstrukce a  extenzní metody by šlo určitě vylepšit a vytunit. Nemyslím si a nikdy jsem si narozdíl od některých rozjuchaných "VsechnoSLinqemJeTedCoolTyRetarde" MSDN blogů nemyslel, že LINQ a extenzní metody jsou univerzální kladivo na každý problém universa, včetně precizní analýzy finální odpovědi '42' , ale jako příklad, co lze s těmito nástroji dělat, mi Dijkstrův algoritmus přišel zajímavý.

Update 12. 2.:

Petr poptával v komentářích zdrojové kódy. Zde jsou.